Mechanics of Growth and Remodeling
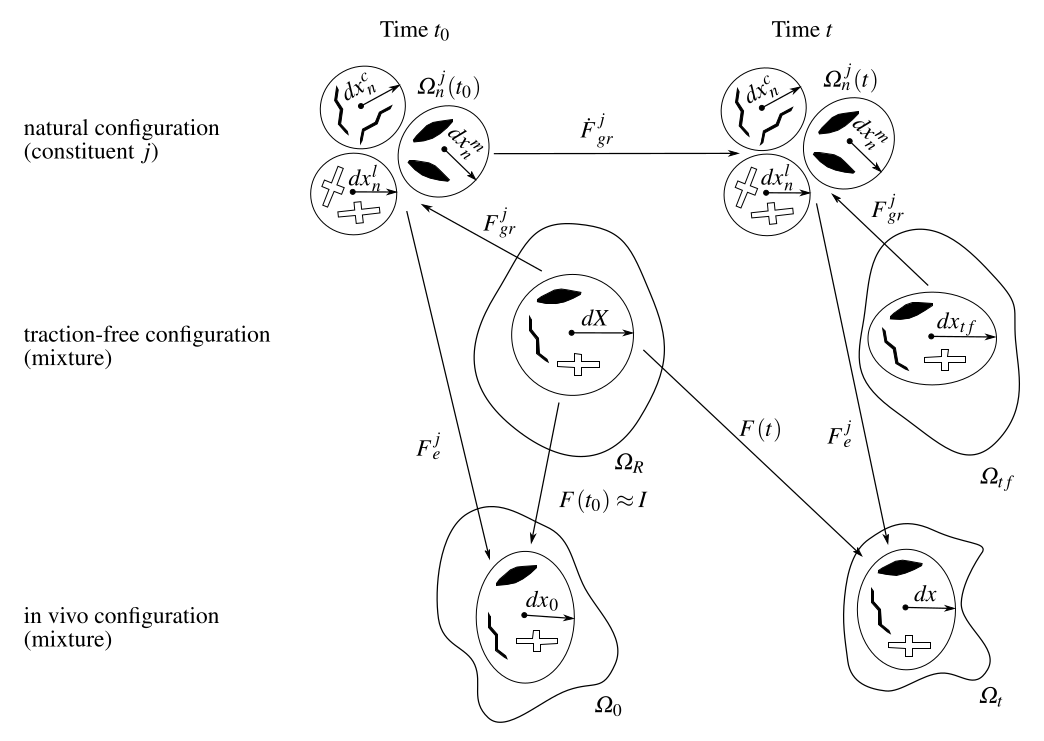
Let us consider a material mixture composed by several constituents (\(j=1,2,...,n\)) in its hypothetical traction-free reference configuration \(\Omega_R\subset\mathbb{R}^3\) and subsequently deformed into a loaded configuration \(\Omega_t\subset\mathbb{R}^3\) at time \(t\geq0\). Each material point \(\pmb{X}\in\Omega_R\) is mapped to the corresponding spatial point \(\pmb{x}(\pmb{X},t)\in\Omega_t\) by \(\pmb{x}:\mathbb{R}^{+}\times\Omega_R\rightarrow\mathbb{R}^3\). This allow to define the total deformation of the mixture as
\[\pmb{F} = \frac{\partial\pmb{x}}{\partial\pmb{X}} \mbox{ with } J = det(\pmb{F}),\]where \(\pmb{F}\) is the deformation gradient of the mixture and incorporate elastic (\(\pmb{F}^j_e\)) and inelastic (\(\pmb{F}^j_{gr}\)) deformations for each \(j\)th constituent of the material,
\[\pmb{F} = \pmb{F}^j_{e} \pmb{F}^j_{gr}.\]It is assumed that each constituent of the mixture is hyperelastic and their potential elastic energy depends only on the elastic deformations (\(\Psi^j=\Psi^j(\pmb{C}^j_e)\)). We can define the second Piola-Kirchhoff stress tensor of the \(j\)th contituent as,
\[\pmb{S}^j = 2\frac{\varrho^j_R}{\phi^j}\frac{\partial\Psi^j}{\partial\pmb{C}} = 2\frac{\varrho^j_R}{\phi^j}\frac{\partial\Psi^j}{\partial\pmb{C}^j_e}: \frac{\partial\pmb{C}^j_e}{\partial\pmb{C}}\]where \(\pmb{C}^j_e\) is the elastic right Cauchy-Green tensor obtained from the total right Cauchy-Green tensor \(\pmb{C}=\pmb{F}^T\pmb{F}\) and the decomposition of the deformation \(\pmb{F}\),
\[\pmb{C}^j_e = [\pmb{F}^j_{gr}]^{-T} \pmb{C} [\pmb{F}^j_{gr}]^{-1};\]\(\phi^j=\frac{\varrho^j_R}{\varrho_R}\) is the constituent mass fraction, \(\varrho_R\) is the mixture density in reference configuration and \(\varrho^j_R\) is the \(j\)th constituent density in reference configuration.
Thus applying the rule of mixtures, the total mass density is the additon of the constituent densities (\(\varrho_R=\sum\varrho^j_R\)). And in the same way the material stress is the addition of the constituent stresses (\(\pmb{S}=\sum\phi^j\pmb{S}^j\)), where the stress can be mapped to the spatial configuration by the push-forward transformation,
\[\pmb{\sigma}^j = \frac{1}{J}\pmb{F}\pmb{S}^j\pmb{F}^T,\]allowing to write the total mixture spatial stress as \(\pmb{\sigma}=\sum\phi^j\pmb{\sigma}^j\).
During Growth and Remodeling (G&R) the tissue is continuously adapting and consequently is changing its structure with deposition/removal of mass of the contituents, for instance, elastin degradation, SMC apoptosis/proliferation or collagen production. The mass changes in the mixture can be written like,
\[\dot{m} = \frac{D}{Dt}(\varrho_R V) = \frac{D}{D}(\varrho v),\]where \(\dot{m}\) is the deposition/removal of mass in the mixture. Where the reference volume \(V\) does not change, the spatial density \(\varrho\) is homogeneous and constant in time, and the spatial volume \(v\) is related to the reference volume by \(v=JV\). Therefore, the conservation of mass can be rewritten as,
\[\frac{\partial\varrho_R}{\partial t} = \varrho J div(\pmb{v}).\]We have to remark that in the G&R framework the reference mass density (per unit reference volume) evolves and it is time dependent \(\varrho_R=\varrho_R(t)\).
Furthermore, it can be assumed that G&R is an slow process and have place in long time scales. Then it can be assumed that the G&R is quasi-static and the conservation of linear momentum equals zero,
\[\frac{D}{D t} (\varrho\pmb{v}) = div(\pmb{\sigma}) + \varrho\pmb{b} = 0,\]where \(\pmb{v}\) is the velocity of the body \(\Omega_t\) and \(\pmb{b}\) is the body force.